Angles of Elevation and Depression

Chapter 51

Concept Explanation:

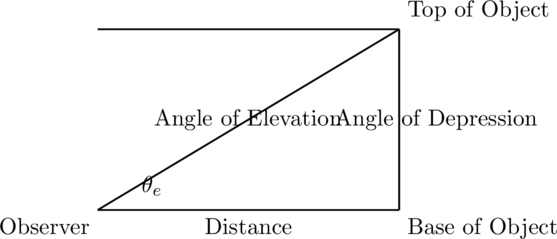
Angles of elevation and depression are concepts used in trigonometry to measure the angle formed between a horizontal line and a line of sight. These angles are frequently used in real-life problems involving heights and distances, such as determining how high an object is above ground level or how far away an object is.

Angle of Elevation: This is the angle formed between the horizontal line of sight and the upward line of sight when looking at an object above the horizontal. For example, if you’re looking at the top of a building from the ground, the angle between your line of sight and the horizontal is the angle of elevation.
Angle of Depression: This is the angle formed between the horizontal line of sight and the downward line of sight when looking at an object below the horizontal. For instance, if you’re standing on a cliff and looking down at the base, the angle between your line of sight and the horizontal is the angle of depression.

The key here is that the angle of elevation and the angle of depression are always measured from the horizontal, and the angle of elevation is equal to the angle of depression due to the alternate interior angles formed by the horizontal line.

Common Mistakes:

Confusing Elevation with Depression: Students often mix up which angle is elevation and which is depression. Remember: elevation is “up,” and depression is “down.”
Incorrect Triangle Set-Up: It’s common to misidentify the sides of the triangle in word problems, leading to incorrect trigonometric equations. Always make sure to correctly label the adjacent, opposite, and hypotenuse sides.
Assuming Right Angles: Not all problems explicitly state that a right angle is formed. Be sure to check the problem carefully before assuming the presence of a right triangle.

Helpful Tips:

Use a Diagram: Always draw a diagram for these types of problems. Label the angle of elevation or depression, the distance or height, and the sides of the triangle.
Trigonometric Functions: The sine, cosine, and tangent functions are your best friends for solving these problems. Always set up the appropriate trigonometric ratio depending on the sides and angles given.

Diagrams:

Here is an illustration showing the angles of elevation and depression in a typical word problem scenario.

Hard Questions:

Q1: From a point 50 meters away from the base of a building, the angle of elevation to the top of the building is $30^\circ$ . How tall is the building?

Step-by-Step Solution:

Diagram Setup: Draw a right triangle where the distance from the point to the base is the adjacent side, the height of the building is the opposite side, and the angle of elevation is $30^\circ$ .
Trigonometric Function: Use the tangent function since you know the angle and the adjacent side, and you are solving for the opposite side.

$\tan(30^\circ) = \frac{\text{Height}}{50}$

Solve for Height:

$\text{Height} = 50 \times \tan(30^\circ)$

$\text{Height} = 50 \times 0.577 = 28.87 \, \text{meters}$

Answer:

The height of the building is approximately 28.87 meters.

Q2: A person is standing on a cliff that is 100 meters high. The angle of depression from the person to a boat on the water is $20^\circ$ . How far is the boat from the base of the cliff?

Step-by-Step Solution:

Diagram Setup: Draw a right triangle where the height of the cliff is the opposite side, the distance from the boat to the base is the adjacent side, and the angle of depression is $20^\circ$ .
Trigonometric Function: Use the tangent function.

$\tan(20^\circ) = \frac{100}{\text{Distance}}$

Solve for Distance:

$\text{Distance} = \frac{100}{\tan(20^\circ)}$

$\text{Distance} = \frac{100}{0.364} = 274.73 \, \text{meters}$

Answer:

The boat is approximately 274.73 meters from the base of the cliff.

Q3: A ladder leans against a building, forming an angle of elevation of $45^\circ$ with the ground. If the ladder is 10 meters long, how high does the ladder reach on the building?

Step-by-Step Solution:

Diagram Setup: Draw a right triangle where the length of the ladder is the hypotenuse, the height it reaches is the opposite side, and the angle of elevation is $45^\circ$ .
Trigonometric Function: Use the sine function.

$\sin(45^\circ) = \frac{\text{Height}}{10}$

Solve for Height:

$\text{Height} = 10 \times \sin(45^\circ)$

$\text{Height} = 10 \times 0.707 = 7.07 \, \text{meters}$

Answer:

The ladder reaches approximately 7.07 meters on the building.

Q4: A pilot flying at an altitude of 1,200 meters sees the airport at an angle of depression of $15^\circ$ . What is the horizontal distance between the plane and the airport?

Step-by-Step Solution:

Diagram Setup: The altitude of the plane is the opposite side, and the horizontal distance is the adjacent side of the right triangle.
Trigonometric Function: Use the tangent function.

$\tan(15^\circ) = \frac{1200}{\text{Distance}}$

Solve for Distance:

$\text{Distance} = \frac{1200}{\tan(15^\circ)}$

$\text{Distance} = \frac{1200}{0.268} = 4477.61 \, \text{meters}$

Answer:

The horizontal distance between the plane and the airport is approximately 4477.61 meters.

Q5: From a lighthouse that is 60 meters above sea level, the angle of depression to a ship is $25^\circ$ . How far is the ship from the base of the lighthouse?

Step-by-Step Solution:

Diagram Setup: The height of the lighthouse is the opposite side, and the distance to the ship is the adjacent side of the triangle.
Trigonometric Function: Use the tangent function.

$\tan(25^\circ) = \frac{60}{\text{Distance}}$

Solve for Distance:

$\text{Distance} = \frac{60}{\tan(25^\circ)}$

$\text{Distance} = \frac{60}{0.466} = 128.8 \, \text{meters}$

Answer:

The ship is approximately 128.8 meters from the base of the lighthouse.

Avoiding Common Mistakes:

Using the Wrong Function: Students often confuse sine, cosine, and tangent. Remember that tangent involves the opposite and adjacent sides, while sine and cosine involve the hypotenuse.
Forgetting to Subtract Angles: When working with depression angles, be sure to subtract the angle from 90° to get the correct angle in some cases.
Misinterpreting the Diagram: Always ensure your diagram correctly reflects the problem statement, and double-check which sides correspond to the opposite, adjacent, and hypotenuse.

Helpful Links for Further Study:

[Understanding Angles of Elevation and Depression](https://www.khanacademy.org/math/trigonometry/trig-right-triangles/trig-elevation-depression/v

/angles-of-elevation-and-depression)

Interactive Trigonometry Tools

Understanding angles of elevation and depression and applying trigonometric functions will enable you to solve real-world problems involving heights and distances. Be sure to practice drawing diagrams and identifying the correct trigonometric ratios for different problem setups.

Toll Free: 1 (888) 356-0607