Adjoint of a Matrix

Chapter 35

Adjoint of a Matrix Concept Explanation:

The adjoint of a matrix (also called the adjugate) is the transpose of the cofactor matrix. It is used in finding the inverse of a matrix. If a matrix $A$ is $2 \times 2$ or $3 \times 3$ , the steps are as follows:

Find the Cofactor Matrix: Calculate the cofactor for each element of the matrix.
Transpose the Cofactor Matrix: Swap the rows and columns to get the adjoint.

For example, if $A = \begin{pmatrix} a & b \ c & d \end{pmatrix}$ , the adjoint $\text{Adj}(A)$ is:

$\text{Adj}(A) = \begin{pmatrix} d & -b \ -c & a \end{pmatrix}$

Common Mistakes:

Sign Errors: Students often make mistakes when calculating the cofactors, especially in managing signs.
Transpose Errors: Failing to correctly transpose the cofactor matrix can lead to an incorrect adjoint.

Helpful Tips:

Double-Check Cofactor Signs: Be careful with the signs when calculating cofactors.
Transpose Carefully: Take your time transposing the matrix to avoid mistakes.

Hard Questions:

Q1: Find the adjoint of $A = \begin{pmatrix} 1 & 2 \ 3 & 4 \end{pmatrix}$ .

Step-by-Step Solution:

Find the cofactor matrix:

$\text{Cofactor}(A) = \begin{pmatrix} 4 & -2 \ -3 & 1 \end{pmatrix}$

Transpose the cofactor matrix:

$\text{Adj}(A) = \begin{pmatrix} 4 & -3 \ -2 & 1 \end{pmatrix}$

Answer:

The adjoint of 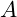$A$ is $\begin{pmatrix} 4 & -3 \ -2 & 1 \end{pmatrix}$ .

Q2: Find the adjoint of $A = \begin{pmatrix} 2 & 0 \ 1 & 3 \end{pmatrix}$ .

Step-by-Step Solution:

Find the cofactor matrix:

$\text{Cofactor}(A) = \begin{pmatrix} 3 & 0 \ -1 & 2 \end{pmatrix}$

Transpose the cofactor matrix:

$\text{Adj}(A) = \begin{pmatrix} 3 & -1 \ 0 & 2 \end{pmatrix}$

Answer:

The adjoint of 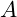$A$ is $\begin{pmatrix} 3 & -1 \ 0 & 2 \end{pmatrix}$ .

Q3: Find the adjoint of $A = \begin{pmatrix} 0 & 5 \ 2 & -1 \end{pmatrix}$ .

Step-by-Step Solution:

Find the cofactor matrix:

$\text{Cofactor}(A) = \begin{pmatrix} -1 & -5 \ -2 & 0 \end{pmatrix}$

Transpose the cofactor matrix:

$\text{Adj}(A) = \begin{pmatrix} -1 & -2 \ -5 & 0 \end{pmatrix}$

Answer:

The adjoint of 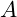$A$ is $\begin{pmatrix} -1 & -2 \ -5 & 0 \end{pmatrix}$ .

Toll Free: 1 (888) 356-0607