Absolute Value Inequalities Concept Explanation:
An absolute value inequality is of the form ![]() or
or ![]() , where
, where ![]() is a non-negative number. The two types of absolute value inequalities have different interpretations:
is a non-negative number. The two types of absolute value inequalities have different interpretations:
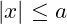 : This means
: This means  . The solution is a range of values between
. The solution is a range of values between  and
and 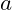 .
.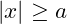 : This means
: This means  or
or 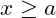 . The solution is outside the interval
. The solution is outside the interval 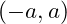 .
.
Diagram:
Here’s a diagram to illustrate the solutions to the inequality ![]() :
:
![]()
The solution is all values between ![]() and
and ![]() .
.
Hard Questions:
Q1: Solve the inequality ![]() .
.
Step-by-Step Solution:
Rewrite the absolute value inequality as a compound inequality:
Subtract 2 from all parts of the inequality:
Answer:
- The solution is
.
Q2: Solve the inequality .
Step-by-Step Solution:
The absolute value inequality means:
Solve both inequalities:
, so
, so
Answer:
- The solution is
or
.
Q3: Solve .
Step-by-Step Solution:
Rewrite the inequality as:
Subtract 1 from all parts:
Now divide by 2:
Answer:
- The solution is
.
