Absolute Value Concept Explanation:
The absolute value of a number represents its distance from zero on the number line, regardless of direction. It’s always a non-negative number.
- For any real number ( x ), the absolute value is denoted as ( |x| ).
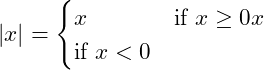
A number line to illustrate the absolute value of ( x = 3 ) and ( x = -3 ):
Diagram:
![]()
Both ( 3 ) and ( -3 ) are 3 units away from zero, so their absolute values are equal.
Hard Questions:
Q1: Find ( |5 – 7| ).
Step-by-Step Solution:
We can rewrite ( |5 – 7| ) as ( |-2| ). Since the absolute value of a negative number is its positive counterpart:
Answer:
- ( |5 – 7| = 2 )
Q2: Solve the equation ( |x + 3| = 8 ).
Step-by-Step Solution:
The absolute value equation ( |x + 3| = 8 ) has two possible solutions:
- ( x + 3 = 8 ) or ( x + 3 = -8 )
Solving both:
- ( x + 3 = 8 ) gives ( x = 5 )
- ( x + 3 = -8 ) gives ( x = -11 )
Answer:
- The solutions are ( x = 5 ) and ( x = -11 ).
Q3: Find the solution set for the inequality ( |2x – 5| \leq 9 ).
Step-by-Step Solution:
We rewrite the absolute value inequality as a compound inequality:
First, solve for ( x ):
Answer:
- The solution set is
