Chapter 35
Adjoint of a Matrix Concept Explanation:
The adjoint of a matrix (also called the adjugate) is the transpose of the cofactor matrix. It is used in finding the inverse of a matrix. If a matrix ![]() is
is ![]() or
or ![]() , the steps are as follows:
, the steps are as follows:
- Find the Cofactor Matrix: Calculate the cofactor for each element of the matrix.
- Transpose the Cofactor Matrix: Swap the rows and columns to get the adjoint.
For example, if ![]() , the adjoint
, the adjoint ![]() is:
is:
![]()
Common Mistakes:
- Sign Errors: Students often make mistakes when calculating the cofactors, especially in managing signs.
- Transpose Errors: Failing to correctly transpose the cofactor matrix can lead to an incorrect adjoint.
Helpful Tips:
- Double-Check Cofactor Signs: Be careful with the signs when calculating cofactors.
- Transpose Carefully: Take your time transposing the matrix to avoid mistakes.
Hard Questions:
Q1: Find the adjoint of .
Step-by-Step Solution:
- Find the cofactor matrix:
Transpose the cofactor matrix:
Answer:
- The adjoint of
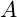 is
is .
Q2: Find the adjoint of .
Step-by-Step Solution:
- Find the cofactor matrix:
Transpose the cofactor matrix:
Answer:
- The adjoint of
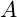 is
is .
Q3: Find the adjoint of .
Step-by-Step Solution:
- Find the cofactor matrix:
Transpose the cofactor matrix:
Answer:
- The adjoint of
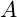 is
is .
