Concept Explanation:
An absolute value function takes the form ![]() , and it creates a V-shaped graph. The graph of
, and it creates a V-shaped graph. The graph of ![]() has the following key features:
has the following key features:
- It is symmetric with respect to the y-axis.
- The vertex of the graph is at
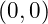 .
. - For
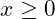 ,
, 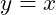 .
. - For
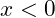 ,
,  .
.
Diagram:
The graph of ![]() :
:
![]()
Hard Questions:
Q1: Sketch the graph of and find its vertex.
Step-by-Step Solution:
The function is a horizontal translation of
![]() shifted 2 units to the right. The vertex is at
shifted 2 units to the right. The vertex is at .
Answer:
- The vertex is at
, and the graph is a V-shape.
Q2: Solve .
Step-by-Step Solution:
The absolute value equation gives two cases:
or
Solving both:
or
Answer:
- The solutions are
and
.
Q3: Find the domain and range of .
Step-by-Step Solution:
The domain of is all real numbers because absolute value functions are defined for all
. The range is
because absolute value functions are non-negative.
Answer:
- The domain is
and the range is
.
