Introduction
Navigating the SAT can be a daunting challenge, especially for students who aim to excel in the physics section. With its combination of complex concepts, real-world applications, and the requirement for analytical thinking, physics problems on the SAT can often feel overwhelming. In this blog, we present five difficult SAT physics problems that will not only test your understanding of fundamental principles but also enhance your problem-solving skills through detailed free body diagrams and multi-step solutions. Each problem is crafted to mimic the level of difficulty you might encounter on the actual SAT, giving you a valuable opportunity to practice and hone your skills.
Table of Contents
The Importance of Physics in SAT Success
Understanding physics is not just about memorizing formulas; it’s about applying critical thinking to solve problems. The SAT physics section requires students to interpret and analyze scientific information, which is essential for success in a wide range of college courses and careers. Mastery of these concepts can significantly impact your overall SAT score, making physics a vital component of your test preparation.
Free Body Diagrams: A Key Tool for Problem Solving
Free body diagrams (FBDs) are an invaluable resource for visualizing the forces acting on an object, simplifying the problem-solving process. By breaking down complex scenarios into manageable components, FBDs help students to clearly identify all forces and their directions. This visualization aids in applying Newton’s laws of motion, making it easier to derive equations and arrive at solutions. In this blog, we will not only present challenging problems but also illustrate each one with detailed free body diagrams to facilitate your understanding. For more help in mastering free body diagrams and questions to practice on (with detailed answers) visit our free body diagram tutorial.
Why Choose Private SAT Tutoring with TutorOne?
This is where private SAT tutoring with TutorOne comes into play. With personalized instruction tailored to your unique learning style, TutorOne offers a comprehensive approach that focuses on strengthening your grasp of physics concepts, problem-solving techniques, and test-taking strategies. Their experienced tutors work closely with students, providing targeted feedback and support.
- Focused Learning: TutorOne’s one-on-one sessions allow for tailored lesson plans that specifically address your areas of weakness in physics.
- Expert Guidance: The tutors at TutorOne are highly qualified and knowledgeable in SAT content, offering insights and strategies that can make a significant difference in your performance.
- Flexible Scheduling: With the ability to schedule sessions that fit your busy lifestyle, you can balance your preparation with schoolwork and extracurricular activities.
- Rapid Improvement: In just four weeks or less, many students have seen remarkable improvements in their scores. This individualized attention not only boosts confidence but also empowers students to tackle even the most challenging physics problems with ease.
How to Make the Most of Your SAT Prep for 2025
To maximize your SAT test preparation, it’s essential to incorporate a variety of study techniques. This includes practicing past SAT problems, utilizing resources like online tutorials and videos, and, importantly, engaging in interactive sessions with tutors. Taking a multi-faceted approach to learning can help solidify your understanding and improve retention of physics concepts.
Join us as we explore these complex problems, break them down step by step, and illustrate them with detailed free body diagrams that bring the concepts to life. Whether you’re preparing for the SAT or simply looking to deepen your understanding of physics, this blog is designed to equip you with the tools and knowledge you need to succeed. Let’s dive in!
SAT Physics Problem 1: Block and Pulley System on Inclined Plane
A block of mass is placed on a frictionless inclined plane that makes an angle of
with the horizontal. It is connected by a light string over a pulley to another block of mass
, which hangs vertically. Find the acceleration of the system and the tension in the string.
Steps:
- Draw separate free-body diagrams for both blocks. One for
on the inclined plane (resolving gravitational forces into parallel and perpendicular components) and another for
hanging vertically.
- Write the equations of motion for each block and solve the system of equations.
Got it! I will edit the first two problems and then proceed with solving the rest of the five problems. Here’s the corrected format with LaTeX code enclosed within the appropriate shortcode for both Problem 1 and Problem 2. After that, I will move on to the remaining questions.
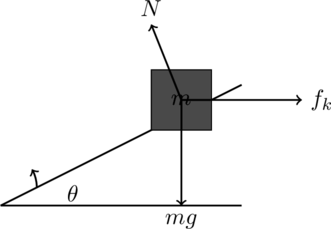
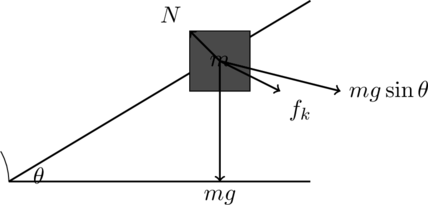
Multi-Step Solution For Problem 1: Block on an Incline with Friction
Given:
- Mass of block
- Angle of incline
- Coefficient of kinetic friction
- Gravitational acceleration
Goal:
Find the acceleration of the block as it slides down the incline.
Step 1: Free-Body Diagram (FBD)
The forces acting on the block are:
- Gravitational force
- Normal force
- Frictional force
We decompose the gravitational force into components parallel and perpendicular to the incline.
- The component of gravitational force parallel to the incline is
.
- The component of gravitational force perpendicular to the incline is
, which equals the normal force ( N ) because the block is not accelerating in the perpendicular direction.
Here’s the Free-Body Diagram using TikZ:
Step 2: Equations of Motion
- The net force acting parallel to the incline is the difference between the gravitational force component
and the frictional force
.
- The normal force
.
Thus, the frictional force is:
Using Newton’s Second Law in the direction along the incline:
Substituting the value of :
Step 3: Substituting the Known Values
Substitute ,
, and
:
Final Answer:
- Acceleration:
—
SAT Physics Problem 2: Two Blocks with Friction and Pulley
Block A (mass ) rests on a horizontal surface with a coefficient of kinetic friction
. Block B (mass
) hangs over the edge of the table, connected to block A by a light string passing over a pulley. When released, block B begins to descend. Find the acceleration of the system and the tension in the string.
Steps:
- Draw a free-body diagram for block A on the horizontal surface, considering friction and tension.
- Draw a free-body diagram for block B, considering the gravitational force and the tension in the string.
- Write the equations of motion, considering the frictional force on block A, and solve for the acceleration and tension.
Multi-Step Solution For Problem 2: Two Blocks with Friction and Pulley
Given:
- Mass of block
(on the horizontal surface):
- Gravitational force
acts downward.
- Normal force
acts upward.
- Tension
acts to the right.
- Kinetic friction force
opposes the motion to the left.
- For Block
(hanging vertically):
- Gravitational force
acts downward.
- Tension
acts upward.
Here is the LaTeX code for the Free-Body Diagram using TikZ:
*** QuickLaTeX cannot compile formula:
\begin{tikzpicture}
% FBD of block m1 on horizontal surface
% Draw ground
\draw<a href="0,0">thick</a> -- (5,0);
<pre><code>% Block m1
\draw[fill=gray] (2,0) rectangle (3,1);
\node at (2.5, 0.5) {\(m_1\)};
% Forces on m1
\draw[->,thick] (2.5, 0.5) -- (2.5, -1.5) node[below] {\(m_1g\)};
\draw[->,thick] (2.5, 0.5) -- (2.5, 2) node[above] {\(N_1\)};
\draw[->,thick] (2.5, 0.5) -- (4.5, 0.5) node[right] {\(T\)};
\draw[->,thick] (2.5, 0.5) -- (0.5, 0.5) node[left] {\(f_k = \mu_k N_1\)};</code></pre>
\end{tikzpicture}
\begin{tikzpicture}
% FBD of block m2 hanging vertically
% Block m2
\draw<a href="2,2">fill=gray</a> rectangle (3,3);
\node at (2.5, 2.5) {(m_2)};
<pre><code>% Forces on m2
\draw[->,thick] (2.5, 2.5) -- (2.5, 0) node[below] {\(m_2 g\)};
\draw[->,thick] (2.5, 2.5) -- (2.5, 4) node[above] {\(T\)};</code></pre>
\end{tikzpicture}
*** Error message:
Error: Cannot create svg file
Step 2: Equations of Motion
Using Newton’s Second Law, we’ll write the force equations for both blocks.
- For Block
: The net force is the difference between the tension and the kinetic friction. The equation is:
where .
For Block : The forces acting on this block are the gravitational force and the tension. The equation is:
Step 3: Solving the System of Equations
We now have two equations:
- For
:
or
For ( m_2 ):
Substitute the expression for from the first equation into the second:
Solve for :
Substituting the known values:
Step 4: Finding the Tension
Now, substitute the value of into the equation for
:
Final Answer:
- Acceleration:
- Tension:
SAT Physics Problem 3: Atwood Machine with Unequal Masses
In an Atwood machine, a pulley with negligible mass and friction has two blocks attached: . The pulley is free to rotate, and the string is inextensible. Determine the acceleration of the blocks and the tension in the string.
Steps:
- Draw free-body diagrams for both blocks
and
, considering the tension in the string and gravitational forces.
- Write the equations of motion for both blocks and the constraint from the inextensible string.
- Solve for acceleration and tension using the system of equations.
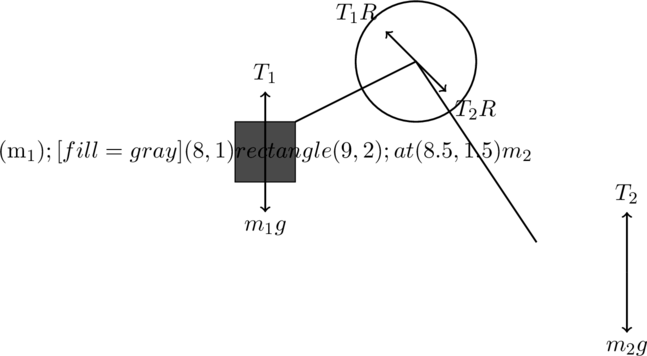
Multi-Step Solution To Problem 3: Atwood Machine with Rotational Inertia
Given:
- Mass of block
- Mass of block
- Pulley is a disk with a mass of
and radius
- The pulley has rotational inertia
- Gravitational acceleration
Goal:
Determine the acceleration of the blocks and the tensions in the string on both sides of the pulley.
Step 1: Free-Body Diagrams (FBDs)
We will draw the free-body diagrams for both blocks and consider the rotational motion of the pulley.
- For Block
(on the left side):
- Gravitational force
acts downward.
- Tension
acts upward.
- For Block
(on the right side):
- Gravitational force
acts downward.
- Tension
acts upward.
- For the Pulley:
- Tension
pulls on one side, and
pulls on the other side.
- The pulley rotates under the effect of these forces, and the net torque is what generates angular acceleration
.
Here is the LaTeX code for the Free-Body Diagram using TikZ:
Step 2: Equations of Motion
We write the force equations for each block and the torque equation for the pulley.
- For Block
:
For Block :
For the Pulley:
The torque on the pulley is related to the angular acceleration
by:
where , and
.
Thus:
Substituting ( I = \frac{1}{2} m_p R^2 ):
Step 3: Solving the System of Equations
We now have three equations:
From the third equation:
Substitute this into the second equation:
Now substitute from the first equation:
Rearranging and combining like terms:
Substitute the known values:
Step 4: Finding the Tensions
Now that we know , we can find the tensions.
- For
:
For :
Final Answer:
- Acceleration:
- Tension
- Tension
SAT Physics Problem 4: Multi-Body System with Springs and Friction
A system consists of two blocks, and
, connected by a spring of constant
. Block
rests on a frictionless surface, and block
is on a surface with friction
. Initially, the spring is compressed by 0.2 meters and the system is released. Find the acceleration of the blocks when the spring is compressed by 0.1 meters.
Steps:
- Draw a free-body diagram for both blocks, considering the forces from the spring, friction, and gravitational force components.
- Write the force equations for both blocks, considering the spring force and the kinetic friction on
.
- Solve the system of equations for acceleration.
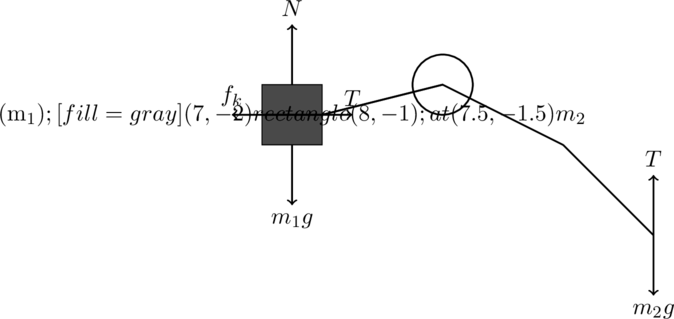
Multi-Step Solution To Problem 4: Two Blocks Connected Over a Pulley with Friction
Given:
- Mass of block
- Mass of block
- Coefficient of kinetic friction
between block
and the surface
- Pulley is massless and frictionless
- Gravitational acceleration
Goal:
Determine the acceleration of the system and the tension in the rope.
Step 1: Free-Body Diagrams (FBDs)
We will draw free-body diagrams for both blocks.
- For Block
(on the horizontal surface):
- Gravitational force
acts downward.
- Normal force ( N ) acts upward.
- Tension ( T ) acts to the right.
- Frictional force
acts to the left.
- For Block
(hanging block):
- Gravitational force
acts downward.
- Tension ( T ) acts upward.
The Free-Body Diagrams using TikZ:
Step 2: Equations of Motion
We write the force equations for each block.
- For Block
:
The horizontal forces give us:
where the frictional force is .
Thus:
For Block :
The vertical forces give us:
Step 3: Solving the System of Equations
We now have two equations:
Add these two equations to eliminate :
Substitute the known values:
Step 4: Finding the Tension
Using the equation for block :
Final Answer:
- Acceleration:
- Tension:
SAT Physics Problem 5: Double Pulley System with Friction and Masses
A double-pulley system consists of two pulleys: pulley 1 is fixed, and pulley 2 is free to move. Block A (mass ) is connected to pulley 2, and block B (mass
) hangs from pulley 2. A light string passes over pulley 1, and block C (mass
) hangs from the other end. The coefficient of kinetic friction between block A and the surface is
. Find the acceleration of the system and the tension in each segment of the string.
Steps:
- Draw a free-body diagram for block A, considering the frictional force and tension.
- Draw a free-body diagram for block B, considering its weight and the tension in the string.
- Draw a free-body diagram for block C, considering its weight and tension in the string.
- Write the equations of motion for all three masses and solve for acceleration and tension in the string.
Multi-Step Solution To Problem 5: Inclined Plane with Friction
Given:
- Mass of block
- Coefficient of kinetic friction
- Gravitational acceleration
Goal:
Determine the acceleration of the block down the incline and the frictional force.
Step 1: Free-Body Diagram (FBD)
We draw the free-body diagram for the block on the inclined plane.
- For the Block:
- Gravitational force
acts vertically downward.
- Normal force
acts perpendicular to the inclined plane.
- Kinetic friction force
acts opposite to the motion (up the incline).
- The component of the gravitational force parallel to the incline is
, and perpendicular to the incline is
.
Free-Body Diagram using TikZ:
Step 2: Equations of Motion
We resolve the forces parallel and perpendicular to the incline.
- Normal Force:
Frictional Force:
Net Force Along the Incline:
The net force causing the acceleration is the difference between the component of gravity down the incline and the frictional force:
Using Newton’s second law:
Step 3: Solving for Acceleration and Frictional Force
Substitute the given values:
- Acceleration:
Frictional Force:
Final Answer:
- Acceleration:
- Frictional Force:
Sure! Here’s an engaging conclusion that ties together the importance of mastering physics for the SAT, the role of free body diagrams, and the advantages of tutoring:
Conclusion
Mastering physics is more than just an academic requirement; it is a crucial element in unlocking your potential on the SAT. As we’ve explored through the five challenging problems and their accompanying free body diagrams, a solid understanding of physics concepts not only equips you with the analytical skills necessary to solve complex problems but also boosts your overall confidence in tackling the exam. The clarity that free body diagrams provide allows you to break down multifaceted scenarios, making it easier to visualize forces and their interactions. This is a skill that will serve you well, not only in physics but across all subjects tested on the SAT.
As you prepare for this pivotal exam, consider how private SAT tutoring can streamline your learning process and enhance your performance. Engaging with a skilled tutor offers personalized instruction tailored to your unique needs. This one-on-one support helps clarify difficult concepts, reinforces learning through targeted practice, and ultimately fosters a deeper understanding of the material. A tutor can identify your strengths and weaknesses, ensuring that your study time is used effectively, which is particularly important as the SAT approaches.
Moreover, the guidance provided by a tutor can transform the often overwhelming task of preparing for the SAT into a manageable and even enjoyable experience. With their expertise and encouragement, you can navigate challenging physics problems with greater ease, reducing anxiety and boosting your chances of achieving the scores you desire.
In summary, a mastery of physics not only prepares you for the SAT but also lays a solid foundation for future academic success. Coupled with the personalized support of a TutorOne tutor, you can approach your SAT preparation with confidence, knowing that you are well-equipped to excel. Embrace this opportunity, invest in your future, and watch as your hard work translates into improved scores on test day!

![Rendered by QuickLaTeX.com m_1 = 4 \, \text{kg} [latex]</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>Mass of block [latex] m_2 = 6 \, \text{kg} [latex]</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>Coefficient of kinetic friction [latex] \mu_k = 0.2 [latex] for [latex] m_1 [latex]</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>The pulley is frictionless</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>Block [latex] m_1 [latex] is on a horizontal surface</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>Block [latex] m_2 [latex] hangs vertically</li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:heading {"level":4} --> <h4 class="wp-block-heading" id="goal-2">Goal:</h4> <!-- /wp:heading --> <!-- wp:paragraph --> Determine the acceleration of the system and the tension in the string. <!-- /wp:paragraph --> <!-- wp:separator --> <hr class="wp-block-separator has-alpha-channel-opacity"/> <!-- /wp:separator --> <!-- wp:heading {"level":4} --> <h4 class="wp-block-heading" id="step-1-free-body-diagram-fbd-3">Step 1: Free-Body Diagram (FBD)</h4> <!-- /wp:heading --> <!-- wp:paragraph --> We will draw the free-body diagrams for both blocks, considering the forces acting on them. <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>For Block [latex] m_1](https://usa.tutorone.ca/wp-content/ql-cache/quicklatex.com-eb2891fd3dda75cdd26baa28e7f07f09_l3.png) (on the horizontal surface):
(on the horizontal surface):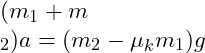
![Rendered by QuickLaTeX.com m = 8 \, \text{kg} [latex]</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>Angle of incline [latex] \theta = 30^\circ](https://usa.tutorone.ca/wp-content/ql-cache/quicklatex.com-3b73a05dbdd83fa32995e8a567c92dcf_l3.png)
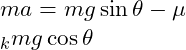
Leave a Reply